BACK
ARITHMETIC PROGRESSION
In an Arithmetic Sequence the difference between one term and the next is a constant.
In other words, we just add the same value each time ... infinitely.
Example:
| 1, 4, 7, 10, 13, 16, 19, 22, 25, ... |
This sequence has a difference of 3 between each number.
In General we could write an arithmetic sequence like this:
{a, a+d, a+2d, a+3d, ... }
where:
- a is the first term, and
- d is the difference between the terms (called the "common difference")
Example: (continued)
| 1, 4, 7, 10, 13, 16, 19, 22, 25, ... |
Has:
- a = 1 (the first term)
- d = 3 (the "common difference" between terms)
And we get:
{a, a+d, a+2d, a+3d, ... }
{1, 1+3, 1+2×3, 1+3×3, ... }
{1, 4, 7, 10, ... }
Rule
We can write an Arithmetic Sequence as a rule:xn = a + d(n-1)
(We use "n-1" because d is not used in the 1st term).
Example: Write the Rule, and calculate the 4th term for
| 3, 8, 13, 18, 23, 28, 33, 38, ... |
This sequence has a difference of 5 between each number.
The values of a and d are:
- a = 3 (the first term)
- d = 5 (the "common difference")
The Rule can be calculated:
xn = a + d(n-1)
= 3 + 5(n-1)
= 3 + 5n - 5
= 5n - 2
So, the 4th term is:
x4 = 5×4 - 2 = 18
Arithmetic Sequences are sometimes called Arithmetic Progressions (A.P.’s)
Summing an Arithmetic Series
To sum up the terms of this arithmetic sequence:a + (a+d) + (a+2d) + (a+3d) + ...
use this formula:
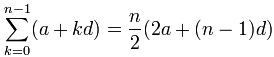
What is that funny symbol? It is called Sigma Notation
| (called Sigma) means "sum up" |
And below and above it are shown the starting and ending values:
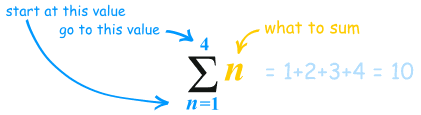
It says "Sum up n where n goes from 1 to 4. Answer=10
Here is how to use it:
Example: Add up the first 10 terms of the arithmetic sequence:
{ 1, 4, 7, 10, 13, ... }
The values of a, d and n are:
- a = 1 (the first term)
- d = 3 (the "common difference" between terms)
- n = 10 (how many terms to add up)
So:
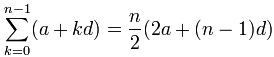
Becomes:
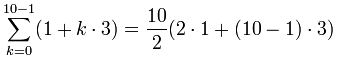
= 5(2+9·3) = 5(29) = 145
Check: why don't you add up the terms yourself, and see if it comes to 145
Why Does the Formula Work?
Let's see why the formula works, because we get to use an interesting "trick" which is worth knowing.First, we will call the whole sum "S":
S = a + (a + d) + ... + (a + (n-2)d) + (a + (n-1)d)
Next, rewrite S in reverse order:
S = (a + (n-1)d) + (a + (n-2)d) + ... + (a + d) + a
Now add those two, term by term:| S | = | a | + | (a+d) | + | ... | + | (a + (n-2)d) | + | (a + (n-1)d) |
| S | = | (a + (n-1)d) | + | (a + (n-2)d) | + | ... | + | (a + d) | + | a |
| 2S | = | (2a + (n-1)d) | + | (2a + (n-1)d) | + | ... | + | (2a + (n-1)d) | + | (2a + (n-1)d) |
Each term is the same! And there are "n" of them so ...
2S = n × (2a + (n-1)d)
Now, just divide by 2 and we get:
S = (n/2) × (2a + (n-1)d)
Which is our formula:
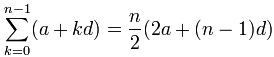
GEOMETRIC PROGRESSION
A geometric sequence is a sequence such that any element after the first is obtained by multiplying the preceding element by a constant called the common ratio which is denoted by r. The common ratio (r) is obtained by dividing any term by the preceding term, i.e.,
where | r | common ratio |
| a1 | first term | |
| a2 | second term | |
| a3 | third term | |
| an-1 | the term before the n th term | |
| an | the n th term |
The geometric sequence is sometimes called the geometric progression or GP, for short.
For example, the sequence 1, 3, 9, 27, 81 is a geometric sequence. Note that after the first term, the next term is obtained by multiplying the preceding element by 3.
The geometric sequence has its sequence formation:
To find the nth term of a geometric sequence we use the formula:
where | r | common ratio |
| a1 | first term | |
| an-1 | the term before the n th term | |
| n | number of terms |
Sum of Terms in a Geometric Progression
Finding the sum of terms in a geometric progression is easily obtained by applying the formulas:
nth partial sum of a geometric sequence
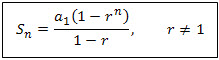
sum to infinity
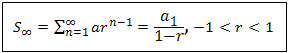
| where | Sn | sum of GP with n terms |
| S∞ | sum of GP with infinitely many terms | |
| a1 | the first term | |
| r | common ratio | |
| n | number of terms |
Examples of Common Problems to Solve
Write down a specific term in a Geometric Progression
Question
Write down the 8th term in the Geometric Progression 1, 3, 9, ...Answer

Finding the number of terms in a Geometric Progression
Question
Answer

Finding the sum of a Geometric Series
Question
Find the sum of each of the geometric series |
Answer

Finding the sum of a Geometric Series to Infinity
Question
Answer
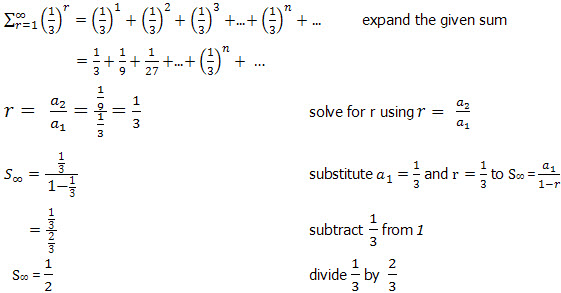


this topic is easy. you can give another example. so that we can practice to solve the question :)
ReplyDelete